
Please remember that these statistics are the mean and standard error of the sample means, not the individual observations.
#Sampling distribution of xbar calculator software#
I also have the simulation software calculate the mean and standard error of the sample means, which should be close to the theoretical values of 100 and 4.743. This setup is basically our previous simulation on steroids! It calculates the sample means and plots them using a histogram. It draws random samples from a population with a mean of 100 and a standard deviation of 15. This simulation follows the same process as the Excel version. I include links for this giftware and my scripts at the end of this post. To perform this simulation, I’ll use the Statistics101 simulation software. This time I’ll draw 500,000 samples instead of just 50. We’ll rerun our previous apple sampling simulation but on a massive scale. Therefore, we’d expect its sampling distribution to center on µ = 100 and that the standard error will be 15 / √10 = 4.743. We used a sample size of 10, which shows up in the standard error of the mean. Recall that we specified that the apple population follows a normal distribution with a mean of 100 and a standard deviation of 15. Now, let’s see how this works using random sampling to see how reality compares. We know what statistical theory and its equation says. Statistics Returning to Our Apple Simulation Related posts: The Normal Distribution and Parameters vs. In summary, sampling distributions center on the population parameter while the standard error defines the width. Because we’re assessing the mean, the variability of that distribution is the standard error of the mean.
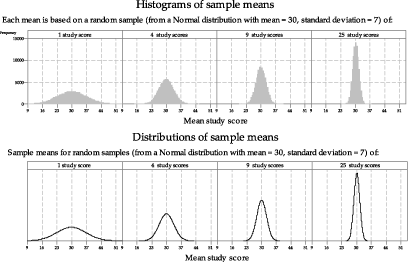
Statisticians refer to the standard deviation for a sampling distribution as the standard error. Additionally, each sampling distribution has a unique spread depending on its sample size. From the formula, we know the variability for a parent distribution differs from its sampling distributions in all cases where n > 1. The variability for the parent distribution is a fixed value (σ), while for a sampling distribution it’s related to σ but also depends on the sample size (n). However, the variabilities are different. Notice how the mean of the parent population is also the central value for the sampling distribution.


 0 kommentar(er)
0 kommentar(er)
